本文共 13025 字,大约阅读时间需要 43 分钟。
简介: bilibili 万亿级传输分发架构的落地,以及 AI 领域如何基于 Flink 打造一套完善的预处理实时 Pipeline。
本文由 bilibili 大数据实时平台负责人郑志升分享,本次分享核心讲解万亿级传输分发架构的落地,以及 AI 领域如何基于 Flink 打造一套完善的预处理实时 Pipeline。本次分享主要围绕以下四个方面:一、B 站实时的前世与今生
二、Flink On Yarn 的增量化管道的方案
三、Flink 和 AI 方向的一些工程实践
四、未来的发展与思考
GitHub 地址
欢迎大家给 Flink 点赞送 star~
一、B 站实时的前世与今生
1. 生态场景辐射
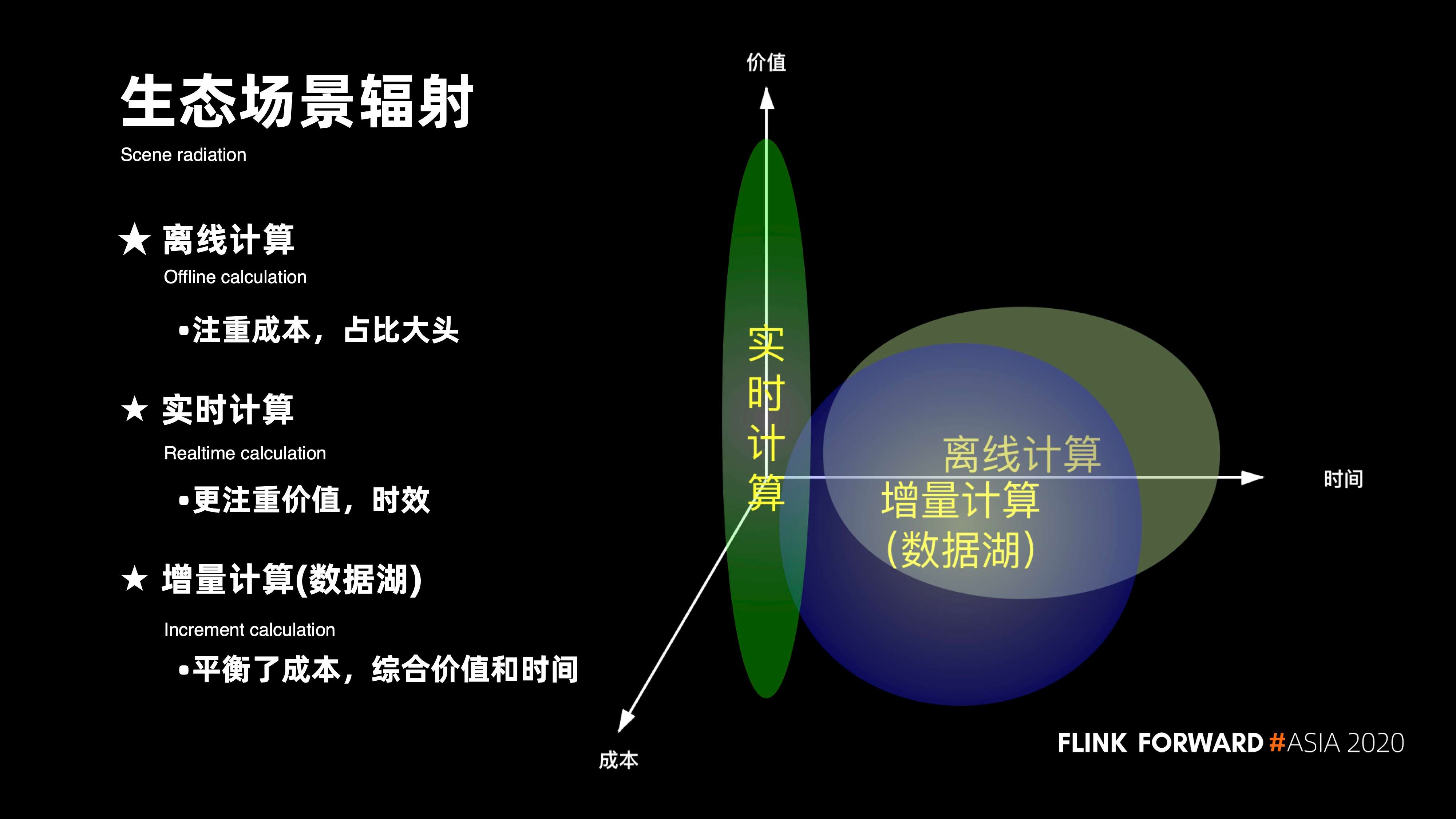
说起实时计算的未来,关键词就在于数据的实效性。首先从整个大数据发展的生态上,来看它的核心场景辐射:在大数据发展的初期,核心是以面向天为粒度的离线计算的场景。 那时候的数据实效性多数都是以运算以天为单位,它更加注重时间和成本的平衡。
随着数据应用,数据分析以及数据仓库的普及与完善,越来越多的人对数据的实效性提出了更高的要求。比如,当需要做一些数据的实时推荐时,数据的实效将决定它的价值。在这种情况下,整个实时计算的场景就普遍诞生。
但在实际的运作过程当中,也遇到了很多场景 ,其实并没有对数据有非常高的实时性要求,在这种情况下必然会存在数据从毫秒,秒或者天的新的一些场景,实时场景数据更多是以分钟为粒度的一些增量计算的场景。对于离线计算,它更加注重成本;对实时计算,它更加注重价值实效;而对于增量计算,它更加注重去平衡成本,以及综合的价值和时间。
2. B 站的时效性
在三个维度上,B 站的划分是怎样的?对于 B 站而言 ,目前有 75% 的数据是通过离线计算来进行支撑的,另外还有 20% 的场景是通过实时计算, 5% 是通过增量计算。
- 对于实时计算的场景, 主要是应用在整个实时的机器学习、实时推荐、广告搜索、数据应用、实时渠道分析投放、报表、olap、监控等;
- 对于离线计算,数据辐射面广,主要以数仓为主;
- 对于增量计算,今年才启动一些新的场景,比如说 binlog 的增量 Upsert 场景。

3. ETL 时效性差
对于实效性问题 ,其实早期遇到了很多痛点 ,核心集中在三个方面:
- 第一,传输管道缺乏计算能力。早期的方案,数据基本都是要按天落到 ODS ,DW 层是凌晨过后的第二天去扫描前一天所有 ODS 层的数据,也就是说,整体数据没办法前置清洗;
- 第二,含有大量作业的资源集中爆发在凌晨之后,整个资源编排的压力就会非常大;
- 第三、实时和离线的 gap 是比较难满足的,因为对于大部分的数据来说,纯实时的成本过高,纯离线的实效又太差。同时,MySQL 数据的入仓时效也不太够。举个例子,好比 B 站的弹幕数据 ,它的体量非常夸张,这种业务表的同步往往需要十几个小时,而且非常的不稳定。

4. AI 实时工程复杂
除了实效性的问题 早期还遇到了 AI 实时工程比较复杂的问题:
- 第一,是整个特征工程计算效率的问题。同样的实时特征的计算场景, 也需要在离线的场景上进行数据的回溯,计算逻辑就会重复开发;
- 第二,整个实时链路比较长。一个完整的实时推荐链路, 涵盖了 N 个实时和 M 个离线的十几个作业组成,有时候遇到问题排查,整个链路的运维和管控成本都非常高;
- 第三、随着 AI 人员的增多,算法人员的投入,实验迭代很难横向扩展。

5. Flink 做了生态化的实践
在这些关键痛点的背景下,我们集中针对 Flink 做了生态化的实践,核心包括了整个实时数仓的应用以及整个增量化的 ETL 管道,还有面向 AI 的机器学习的一些场景。本次的分享会更加侧重增量管道以及 AI 加 Flink 的方向上。下图展示了整体的规模,目前,整个传输和计算的体量,在万亿级的消息规模有 30000+ 计算核数,1000+ job 数以及 100 多个用户。

二、Flink On Yarn 的增量化管道的方案
1. 早期的架构
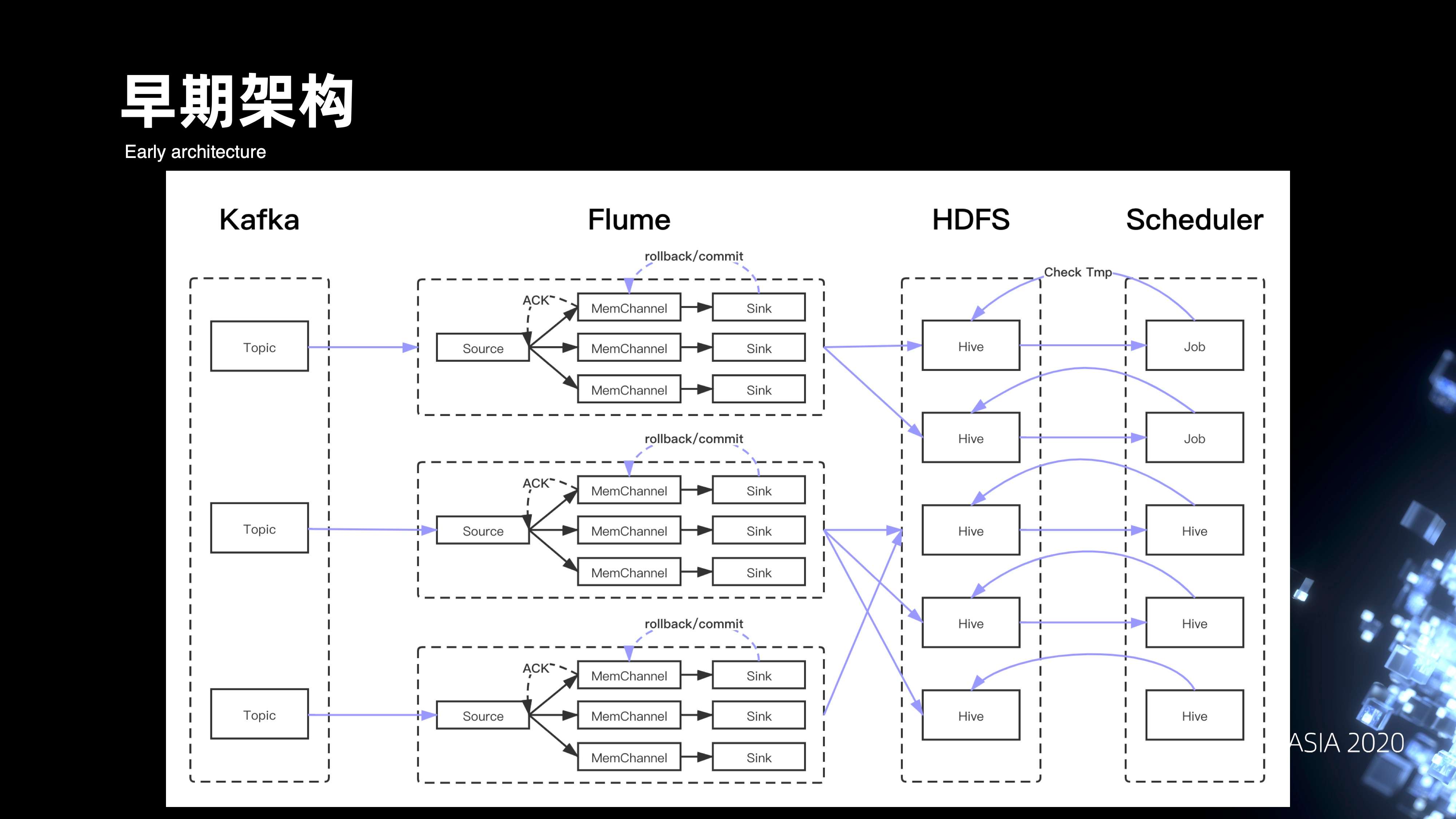
先来看一下整个管道早期的架构,从下图可以看出,数据其实主要是通过 Flume 来消费 Kafka 落到 HDFS。Flume 用它的事务机制,来确保数据从 Source 到 Channel, 再到 Sink 时候的一致性,最后数据落到 HDFS 之后,下游的 Scheduler 会通过扫描目录下有没有 tmp 文件,来判断数据是否 Ready,以此来调度拉起下游的 ETL 离线作业。
2. 痛点
在早期遇到了不少痛点:
-
第一个比较关键的是数据质量。
- 最先用的是 MemoryChannel,它会存在数据的丢失,之后也试过用 FileChannel 的模式,但性能上无法达到要求。此外在 HDFS 不太稳定的情况下,Flume 的事务机制就会导致数据会 rollback 回滚到 Channel,一定程度上会导致数据不断的重复。在 HDFS 极度不稳定的情况下,最高的重复率会达到百分位的概率;
- Lzo 行存储,早期的整个传输是通过分隔符的形式,这种分隔符的 Schema 是比较弱约束的,而且也不支持嵌套的格式。
- 第二点是整个数据的时效,无法提供分钟级的查询,因为 Flume 不像 Flink 有 Checkpoint 斩断的机制,更多是通过 idle 机制来控制文件的关闭;
- 第三点是下游的 ETL 联动。前文有提到,我们更多是通过扫描 tmp 目录是否 ready 的方案,这种情况下 scheduler 会大量的和 NameNode 调用 hadoop list 的 api,这样会导致 NameNode 的压力比较大。

3. 稳定性相关的痛点
在稳定性上也遇到很多问题:
- 第一,Flume 是不带状态的,节点异常或者是重启之后,tmp 没法正常关闭;
- 第二,早期没有依附大数据的环境,是物理部署的模式,资源伸缩很难去把控,成本也会相对偏高;
- 第三,Flume 和 HDFS 在通信上有问题。比如说当写 HDFS 出现堵塞的情况,某一个节点的堵塞会反压到 Channel,就会导致 Source 不会去 Kafka 消费数据,停止拉动 offset,一定程度上就会引发 Kafka 的 Rebalance,最后会导致全局 offset 不往前推进,从而导致数据的堆积。

4. 万亿级的增量管道 DAG 视图
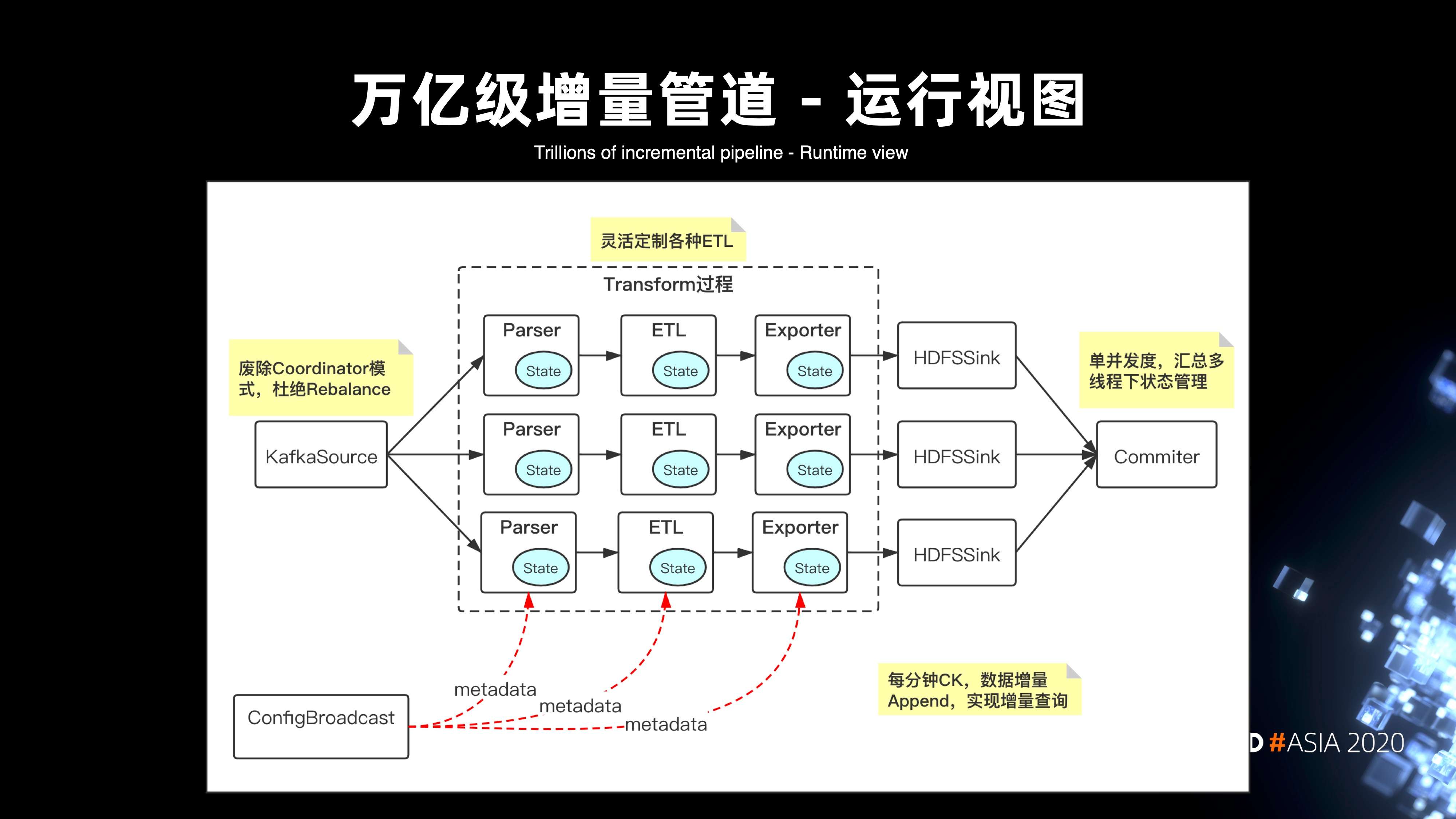
在如上的痛点下,核心方案基于 Flink 构建了一套万亿级的增量管道,下图是整个运行时的 DAG 视图。
首先,在 Flink 架构下,KafkaSource 杜绝了 rebalance 的雪崩问题,即便整个 DAG 视图中有某个并发度出现数据写 HDFS 的堵塞,也不会导致全局所有 Kafka 分区的堵塞。此外的话,整个方案本质是通过 Transform 的模块来实现可扩展的节点。
- 第一层节点是 Parser,它主要是做数据的解压反序列化等的解析操作;
- 第二层是引入提供给用户的定制化 ETL 模块,它可以实现数据在管道中的定制清洗;
- 第三层是 Exporter 模块,它支持将数据导出到不同的存储介质。比如写到 HDFS 时,会导出成 parquet;写到 Kafka,会导出成 pb 格式。同时,在整个 DAG 的链路上引入了 ConfigBroadcast 的模块来解决管道元数据实时更新、热加载的问题。此外,在整个链路当中,每分钟会进行一次 checkpoint,针对增量的实际数据进行 Append,这样就可以提供分钟级的查询。
5. 万亿级的增量管道整体视图
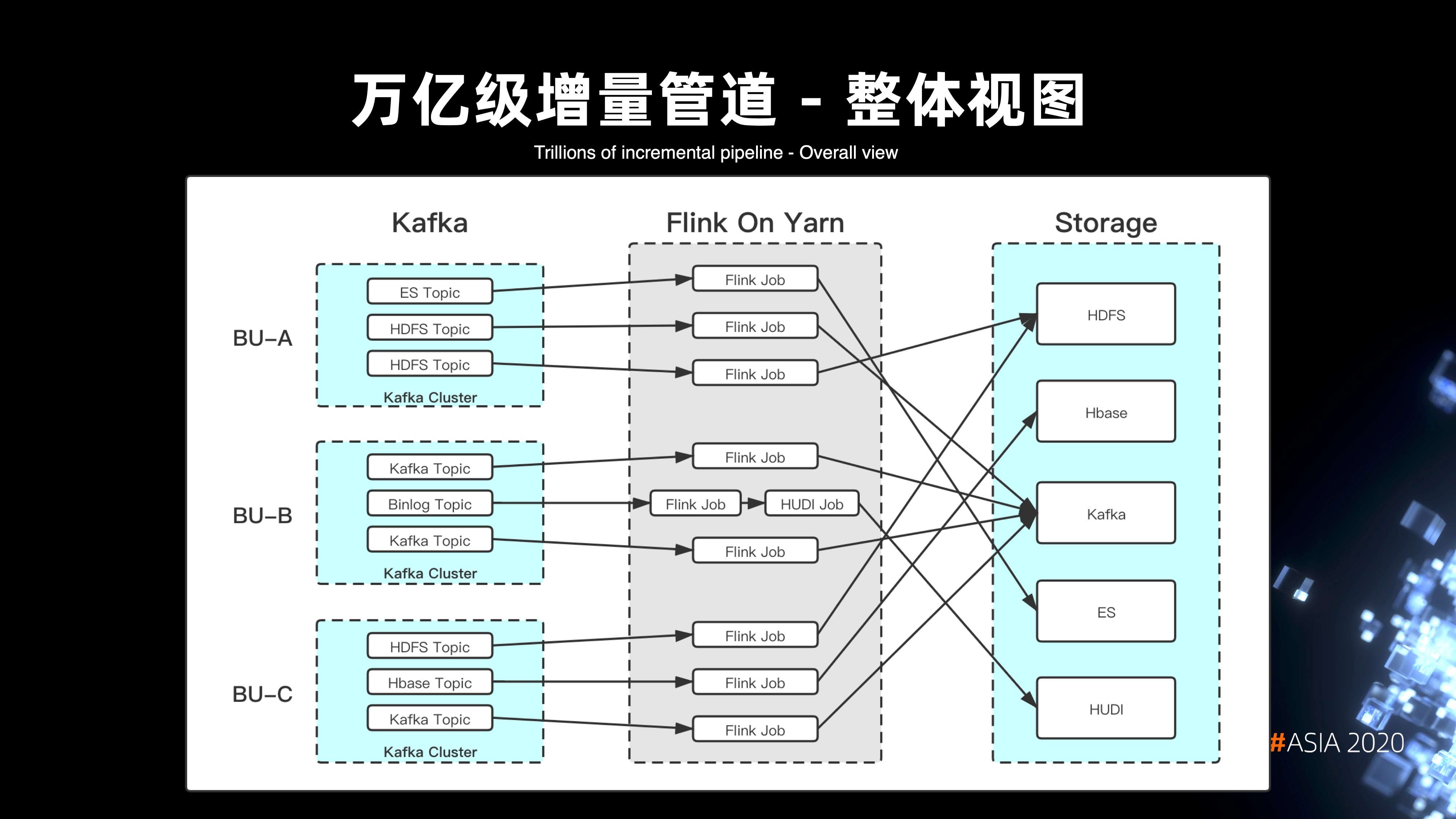
Flink On Yarn 的整体架构,可以看出其实整个管道视图是划分以 BU 为单位的。每个 Kafka 的 topic,都代表了某一种数据终端的分发,Flink 作业就会专门负责各种终端类型的写入处理。视图里面还可以看到,针对 blinlog 的数据,还实现了整个管道的组装,可以由多个节点来实现管道的运作。
6. 技术亮点
接下来来看一下整个架构方案核心的一些技术亮点,前三个是实时功能层面的一些特色,后三个主要是在一些非功能性层面的一些优化。
- 对于数据模型来说,主要是通过 parquet,利用 Protobuf 到 parquet 的映射来实现格式收敛;
- 分区通知主要是因为一条管道其实是处理多条流,核心解决的是多条流数据的分区 ready 的通知机制;
- CDC 管道更多是利用 binlog 和 HUDI 来实现 upsert 问题的解决;
- 小文件主要是在运行时通过 DAG 拓扑的方式来解决文件合并的问题;
- HDFS 通信实际是在万亿级规模下的很多种关键问题的优化;
- 最后是分区容错的一些优化。

6.1 数据模型
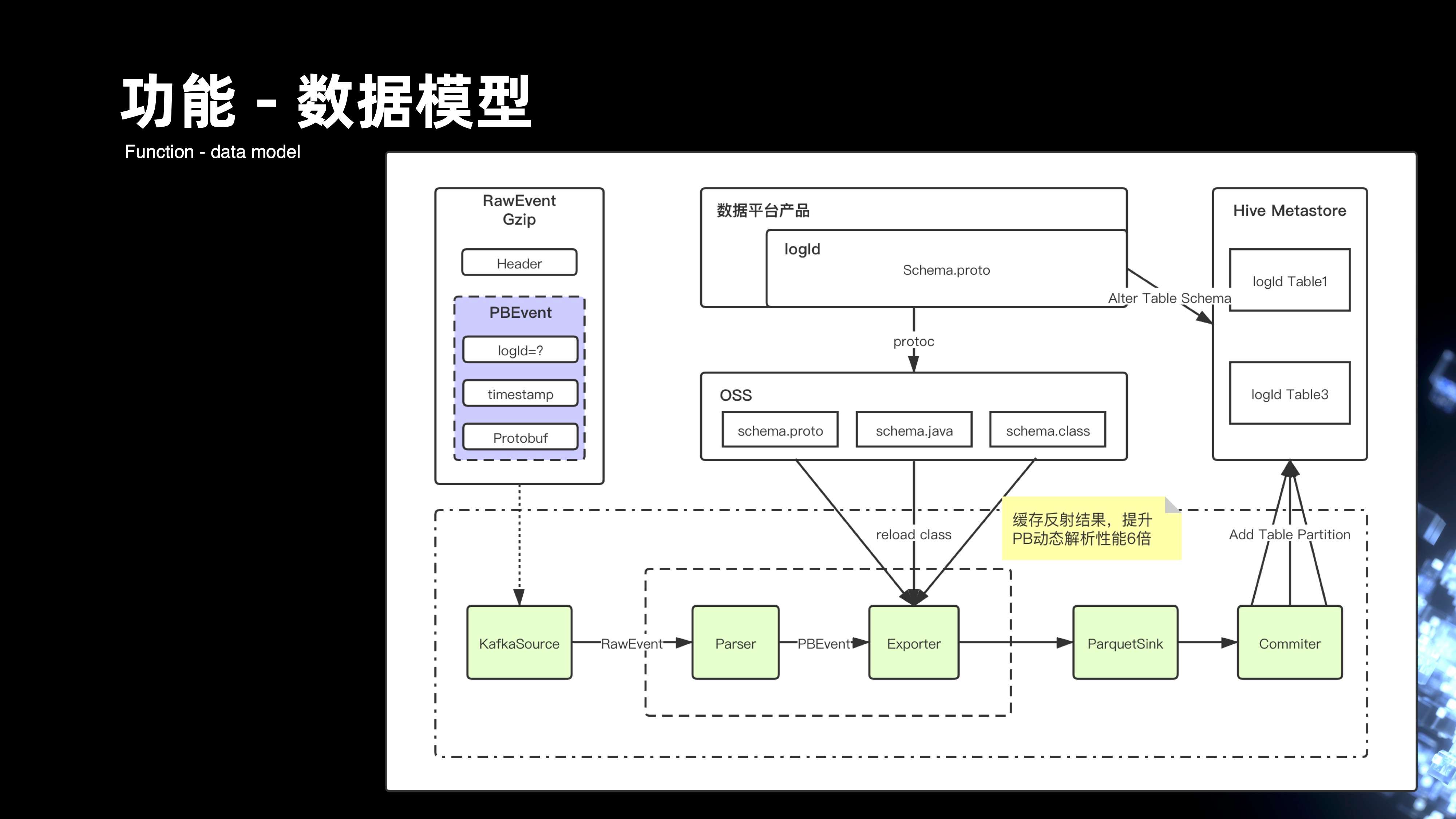
业务的开发主要是通过拼装字符串,来组装数据的一条条记录的上报。后期则是通过了模型的定义和管理,以及它的开发来组织的,主要是通过在平台的入口提供给用户去录制每一条流、每个表,它的 Schema ,Schema 会将它生成 Protobuf 的文件,用户可以在平台上去下载 Protobuf 对应的 HDFS 模型文件,这样,client 端的开发完全就可以通过强 Schema 方式从 pb 来进行约束。
来看一下运行时的过程,首先 Kafka 的 Source 会去消费实际上游传过来的每一条 RawEvent 的记录,RawEvent 里面会有 PBEvent 的对象,PBEvent 其实是一条条的 Protobuf 的记录。数据从 Source 流到的 Parser 模块,解析后会形成 PBEvent,PBEvent 会将用户在平台录入的整个 Schema 模型,存储在 OSS 对象系统上,Exporter 模块会动态去加载模型的变更。然后通过 pb 文件去反射生成的具体事件对象,事件对象最后就可以映射落成 parquet 的格式。这里主要做了很多缓存反射的优化,使整个 pb 的动态解析性能达到六倍的提升。最后,我们会将数据会落地到 HDFS,形成 parquet 的格式。
6.2 分区通知优化
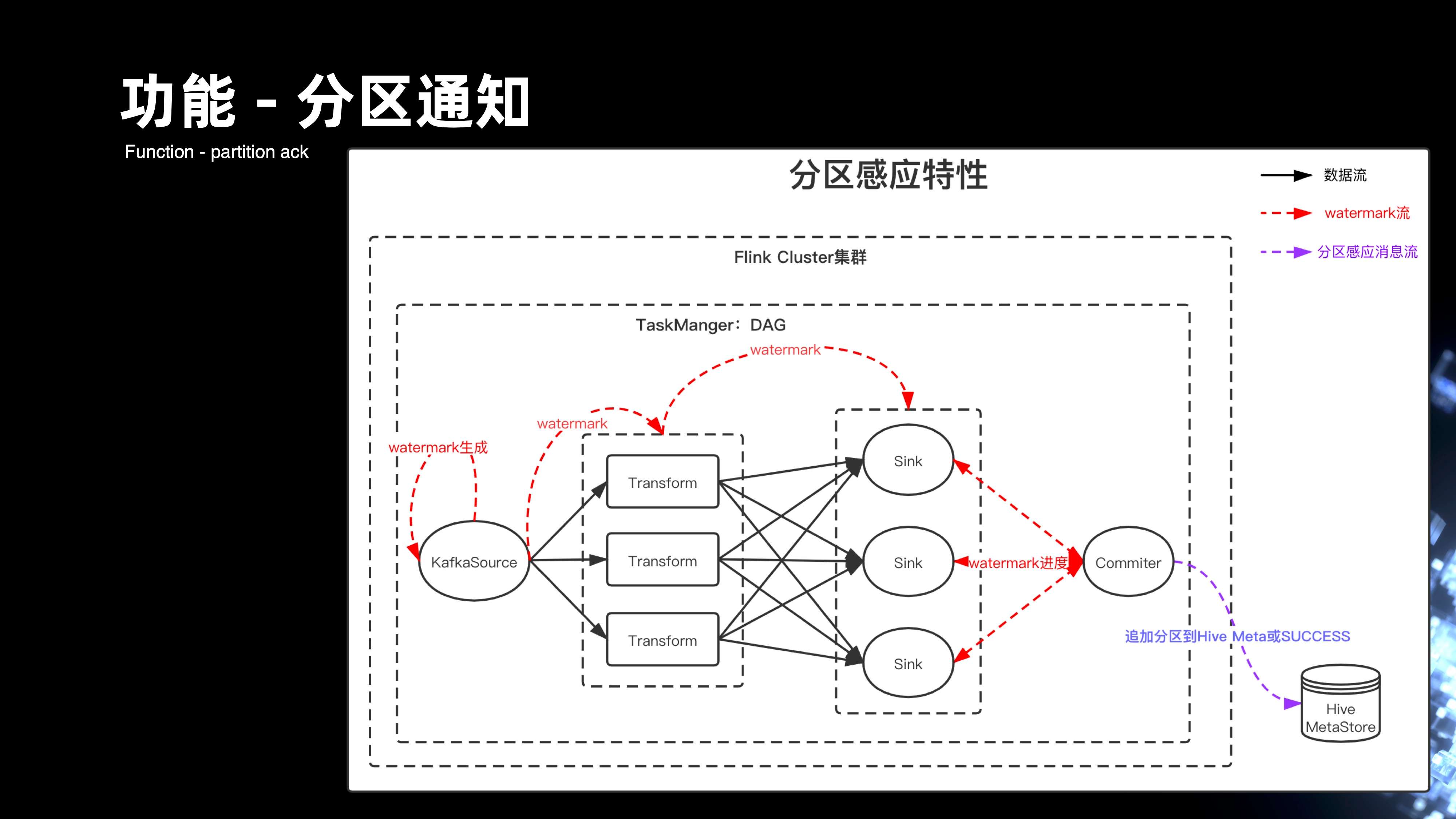
前面提到管道会处理上百条流,早期 Flume 的架构,其实每个 Flume 节点,很难去感应它自己处理的进度。同时,Flume 也没办法做到全局进度的处理。但是基于 Flink,就可以通过 Watermark 的机制来解决。
首先在 Source 会基于消息当中的 Eventime 来生成 Watermark,Watermark 会经过每一层的处理传递到 Sink,最后会通过 Commiter 模块,以单线程的方式来汇总所有 Watermark 消息的进度。当它发现全局 Watermark 已经推进到下个小时的分区的时候,它会下发一条消息到 Hive MetStore,或者是写入到 Kafka, 来通知上小时分区数据 ready,从而可以让下游的调度可以更快的通过消息驱动的方式来拉起作业的运行。
6.3 CDC管道上的优化
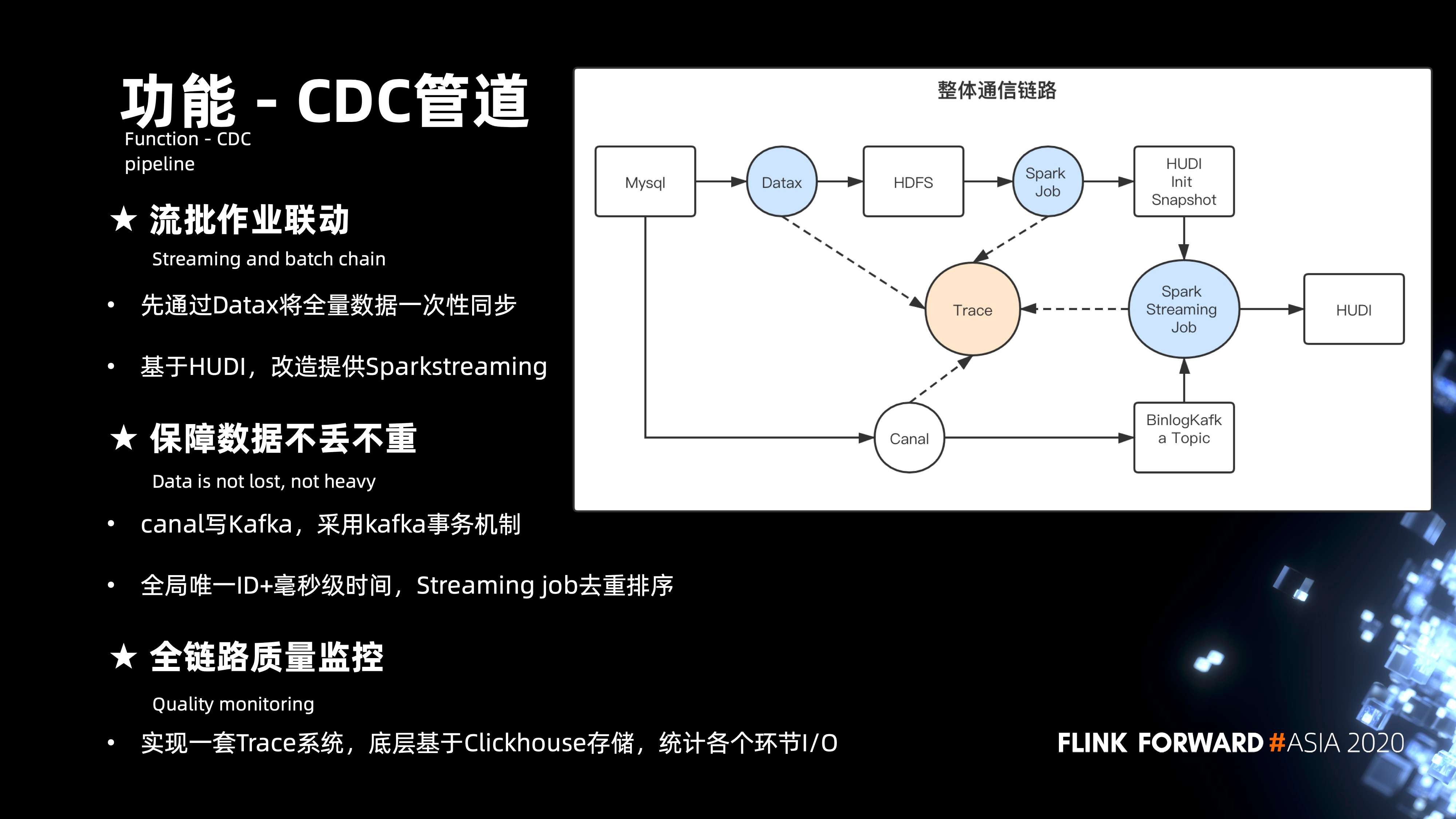
下图右侧其实是整个 cdc 管道完整的链路。要实现 MySQL 数据到 Hive 数据的完整映射,就需要解决流和批处理的问题。
首先是通过 Datax 将 MySQL 的数据全量一次性同步到的 HDFS。紧接着通过 spark 的 job,将数据初始化成 HUDI 的初始快照,接着通过 Canal 来实现将 Mysql 的 binlog 的数据拖到的 Kafka 的 topic,然后是通过 Flink 的 Job 将初始化快照的数据结合增量的数据进行增量更新,最后形成 HUDI 表。
整个链路是要解决数据的不丢不重,重点是针对 Canal 写 Kafka 这块,开了事务的机制,保证数据落 Kafka topic 的时候,可以做到数据在传输过程当中的不丢不重。另外,数据在传输的上层其实也有可能出现数据的重复和丢失,这时候更多是通过全局唯一 id 加毫秒级的时间戳。在整个流式 Job 中,针对全局 id 来做数据的去重,针对毫秒级时间来做数据的排序,这样能保证数据能够有序的更新到的 HUDI。
紧接着通过 Trace 的系统基于 Clickhouse 来做存储,来统计各个节点数据的进出条数来做到数据的精确对比。
6.4 稳定性 - 小文件的合并
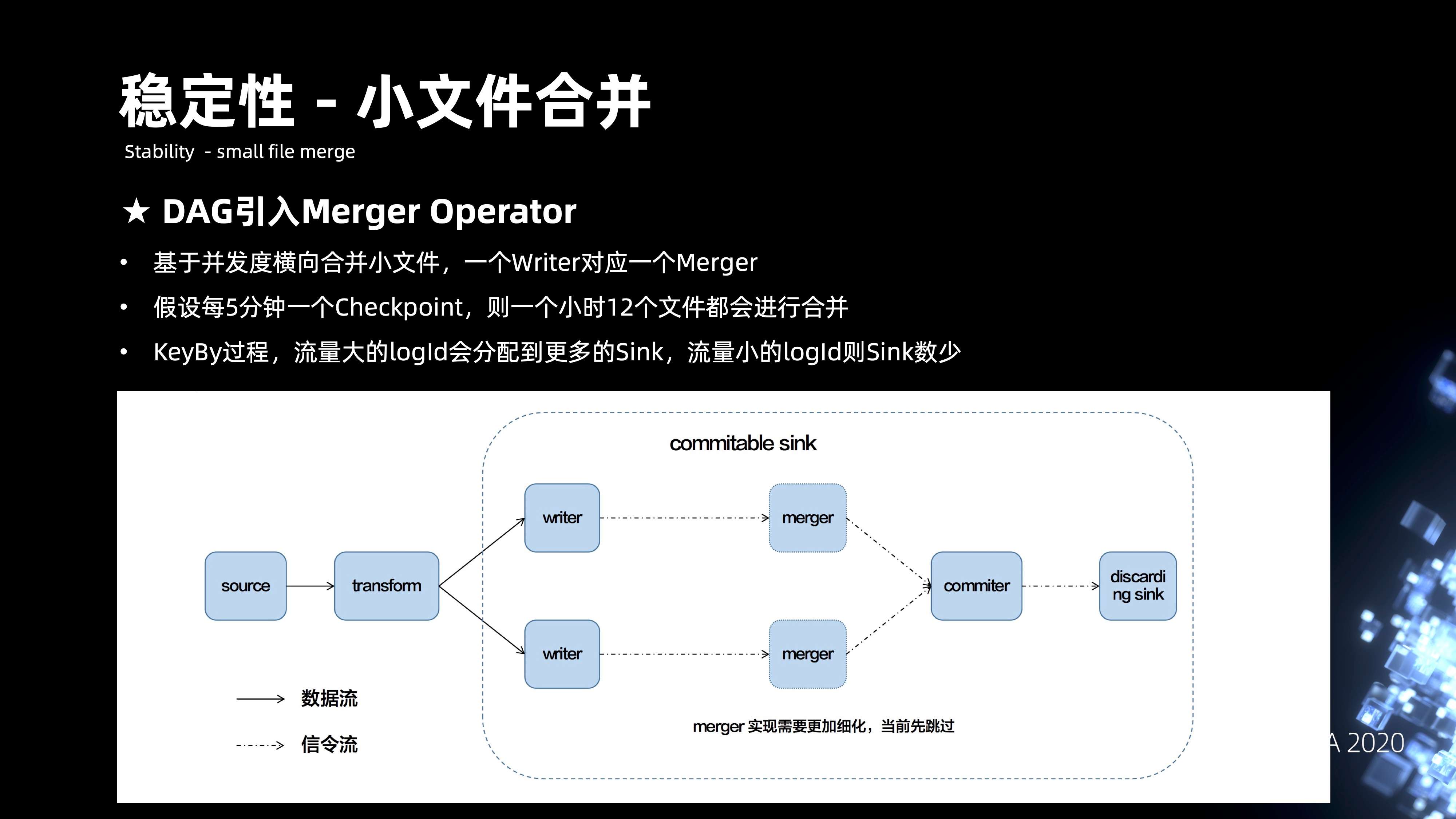
前面提到,改造成 Flink 之后,我们是做了每分钟的 Checkpoint,文件数的放大非常严重。主要是在整个 DAG 当中去引入 merge 的 operater 来实现文件的合并,merge 的合并方式主要是基于并发度横向合并,一个 writer 会对应一个 merge。这样每五分钟的 Checkpoint,1 小时的 12 个文件,都会进行合并。通过种方式的话,可以将文件数极大的控制在合理的范围内。
6.5 HDFS 通信
实际运作过程当中经常会遇到整个作业堆积比较严重的问题,实际分析其实主是和 HDFS 通信有很大的关系。
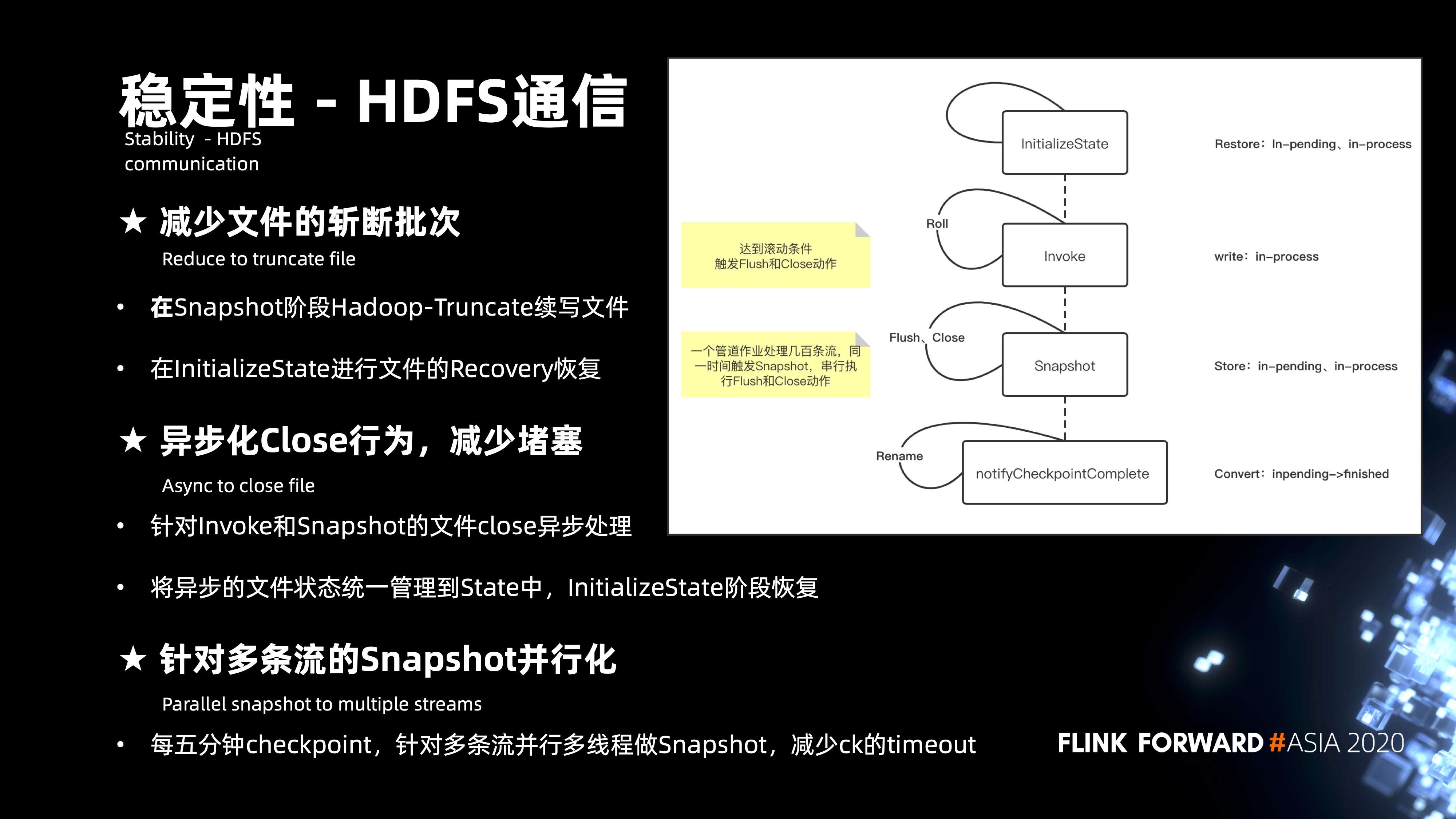
其实 HDFS 通讯,梳理了四个关键的步骤:初始化 state、Invoke、Snapshot 以及 Notify Checkpoint complete。
核心问题主要发生在 Invoke 阶段,Invoke 会达到文件的滚动条件,这时候会触发 flush 和 close。close 实际和 NameNode 通信的时候,会经常出现堵塞的情况。
Snapshot 阶段同样会遇到一个问题,一个管道上百条流一旦触发 Snapshot,串行执行 flush 和 close 也会非常的慢。
核心优化集中在三个方面:
- 第一,减少了文件的斩断,也就是 close 的频次。在 Snapshot 阶段,不会去 close 关闭文件,而更多的是通过文件续写的方式。这样,在初始化 state 的阶段,就需要做文件的 Truncate 来做 Recovery 恢复。
- 第二,是异步化 close 的改进,可以说是 close 的动作不会去堵塞整个总链路的处理,针对 Invoke 和 Snapshot 的 close,会将状态管理到 state 当中,通过初始化 state 来进行文件的恢复。
- 第三,针对多条流,Snapshot 还做了并行化的处理,每 5 分钟的 Checkpoint, 多条流其实就是多个 bucket,会通过循环来进行串行的处理,那么通过多线程的方式来改造,就可以减少 Checkpoint timeout 的发生。
6.6 分区容错的一些优化
实际在管道多条流的情况下,有些流的数据并不是每个小时都是连续的。
这种情况会带来分区,它的 Watermark 没有办法正常推进,引发空分区的问题。所以我们在管道的运行过程当中,引入 PartitionRecover 模块,它会根据 Watermark 来推进分区的通知。针对有些流的 Watermark,如果在 ideltimeout 还没有更新的情况下,Recover 模块来进行分区的追加。它会在每个分区的末尾到达的时候,加上 delay time 来扫描所有流的 Watermark,由此来进行兜底。
在传输过程当中,当 Flink 作业重启的时候,会遇到一波僵尸的文件,我们是通过在 DAG 的 commit 的节点,去做整个分区通知前的僵尸文件的清理删除,来实现整个僵尸文件的清理,这些都属于非功能性层面的一些优化。

三、Flink 和 AI 方向的一些工程实践
1. 架构演进时间表
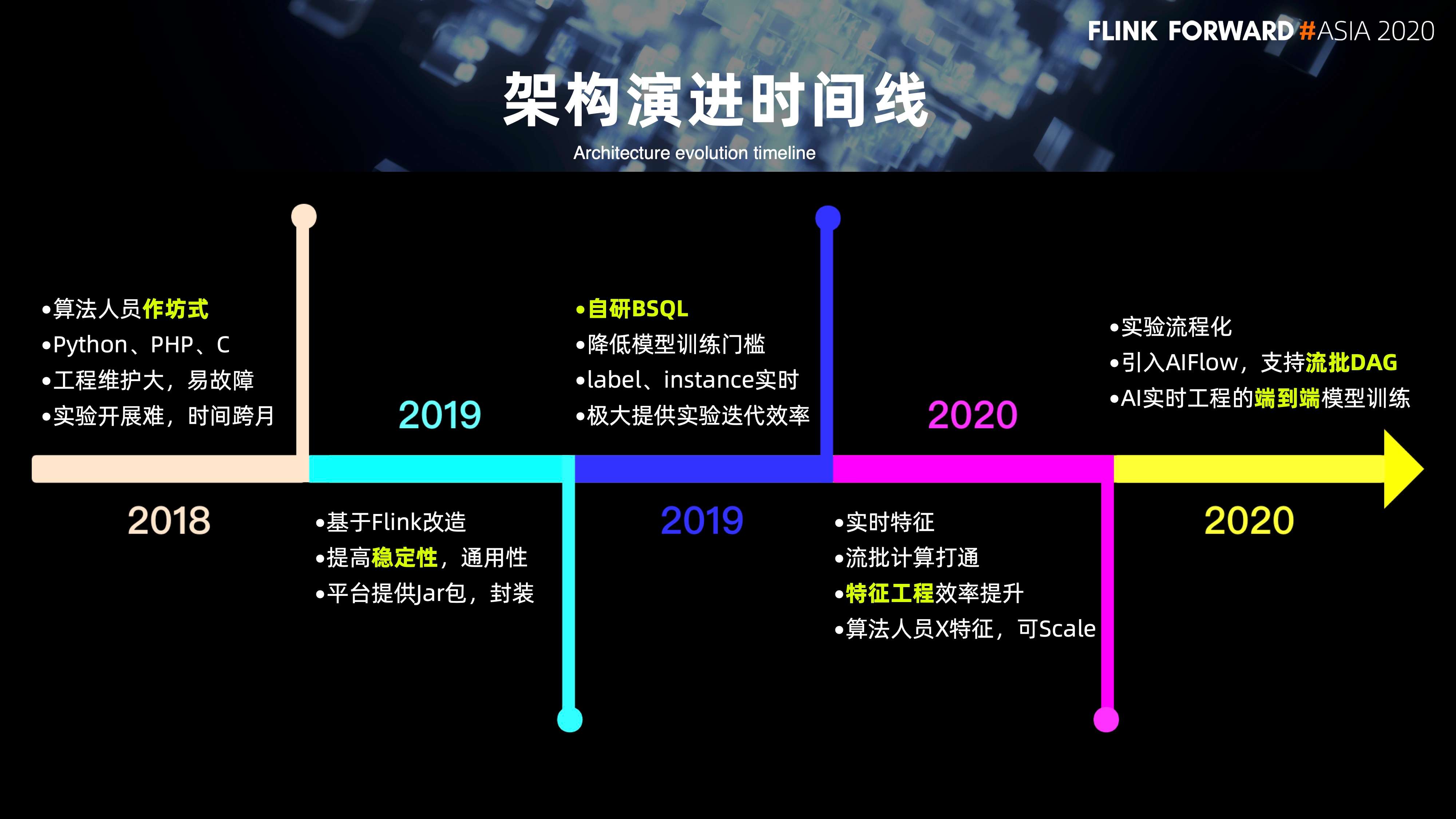
下图是 AI 方向在实时架构完整的时间线。
- 早在 2018 年,很多算法人员的实验开发都是作坊式的。每个算法人员会根据自己熟悉的语言,比如说 Python,php 或 c++ 来选择不同的语言来开发不同的实验工程。它的维护成本非常大,而且容易出现故障;
- 2019 年上半年,主要是基于 Flink 提供了 jar 包的模式来面向整个算法做一些工程的支持,可以说在整个上半年的初期,其实更多是围绕稳定性,通用性来做一些支持;
- 2019 年的下半年,是通过自研的 BSQL,大大降低了模型训练的门槛,解决 label 以及 instance 的实时化来提高整个实验迭代的效率;
- 2020 年上半年,更多是围绕整个特征的计算,流批计算打通以及特征工程效率的提升,来做一些改进;
- 到2020 年的下半年,更多是围绕整个实验的流程化以及引入 AIFlow,方便的去做流批 DAG。
2. AI 工程架构回顾
回顾一下整个 AI 工程,它的早期的架构图其实体现的是整个 AI 在 2019 年初的架构视图,其本质是通过一些 single task 的方式,各种混合语言来组成的一些计算节点,来支撑着整个模型训练的链路拉起。经过 2019 年的迭代,将整个近线的训练完全的替换成用 BSQL 的模式来进行开发和迭代。
3. 现状痛点
在 2019 年底,其实又遇到了一些新的问题,这些问题主要集中在功能和非功能两个维度上。
-
在功能层面:
- 首先从 label 转到产生 instance 流,以及到模型训练,到线上预测,乃至真正的实验效果,整个链路非常的长且复杂;
- 第二,整个实时的特征、离线特征、以及流批的一体,涉及到非常多的作业组成,整个链路很复杂。同时实验和 online 都要做特征的计算,结果不一致会导致最终的效果出现问题。此外,特征存在哪里也不好找,没办法去追溯。

-
在非功能性层面,算法的同学经常会遇到,不知道 Checkpoint 是什么,要不要开,有啥配置。此外,线上出问题的时候也不好排查,整个链路都非常的长。
- 所以第三点就是,完整的实验进度需要涉及的资源是非常多的,但是对算法来说它根本就不知道这些资源是什么以及需要多少,这些问题其实都都对算法产生很大的困惑。
4. 痛点归结
归根结底,集中在三个方面:
- 第一是一致性的问题。从数据的预处理,到模型训练,再到预测,各个环节其实是断层的。当中包括数据的不一致,也包括计算逻辑的不一致;
- 第二,整个实验迭代非常慢。一个完整的实验链路,其实对算法同学来说,他需要掌握东西非常多。同时实验背后的物料没办法进行共享。比如说有些特征,每个实验背后都要重复开发;
- 第三,是运维和管控的成本比较高。
完整的实验链路,背后其实是包含实时的一条工程加离线的一条工程链路组成,线上的问题很难去排查。

5. 实时 AI 工程的雏形
在这样的一些痛点下,在 20 年主要是集中在 AI 方向上去打造实时工程的雏形。核心是通过下面三个方面来进行突破。
- 第一是在 BSQL 的一些能力上,对于算法,希望通过面向 SQL 来开发以此降低工程投入;
- 第二是特征工程,会通过核心解决特征计算的一些问题来满足特征的一些支持;
- 第三是整个实验的协作,算法的目的其实在于实验,希望去打造一套端到端的实验协作,最终希望做到面向算法能够“一键实验”。

6. 特征工程-难点
我们在特征工程中遇到了一些难点。
- 第一是在实时特征计算上,因为它需要将结果利用到整个线上的预测服务,所以它对延迟以及稳定性的要求都非常的高;
- 第二是整个实时和离线的计算逻辑一致,我们经常遇到一个实时特征,它需要去回溯过去 30 天到到 60 天的离线数据,怎么做到实时特征的计算逻辑能同样在离线特征的计算上去复用;
- 第三是整个离线特征的流批一体比较难打通。实时特征的计算逻辑经常会带有窗口时序等等一些流式的概念,但是离线特征是没有这些语义的。

7. 实时特征
这里看一下我们怎么去做实时特征,图中的右侧是最典型的一些场景。比如说我要实时统计用户最近一分钟、6 小时、12 小时、24 小时,对各个 UP 主相关视频的播放次数。针对这样场景,其实里面有两个点:
-
第一、它需要用到滑动窗口来做整个用户过去历史的计算。此外,数据在滑动计算过程当中,它还需要去关联 UP 主的一些基础的信息维表,来获取 UP 主的一些视频来统计他的播放次数。归根结底,其实遇到了两个比较大的痛。
- 用 Flink 原生的滑动窗口,分钟级的滑动,会导致窗口比较多,性能会损耗比较大。
- 同时细粒度的窗口也会导致定时器过多,清理效率比较差。
- 第二是维表查询,会遇到是多个 key 要去查询 HBASE 的多个对应的 value,这种情况需要去支持数组的并发查询。
在两个痛点下,针对滑动窗口,主要是改造成为 Group By 的模式,加上 agg 的 UDF 的模式,将整个一小时、六小时、十二小时、二十四小时的一些窗口数据,存放到整个 Rocksdb 当中。这样通过 UDF 模式,整个数据触发机制就可以基于 Group By 实现记录级的触发,整个语义、时效性都会提升的比较大。同时在整个 AGG 的 UDF 函数当中,通过 Rocksdb 来做 state,在 UDF 当中来维护数据的生命周期。此外还扩展了整个 SQL 实现了数组级别的维表查询。最后的整个效果其实可以在实时特征的方向上,通过超大窗口的模式来支持各种计算场景。

8. 特征-离线
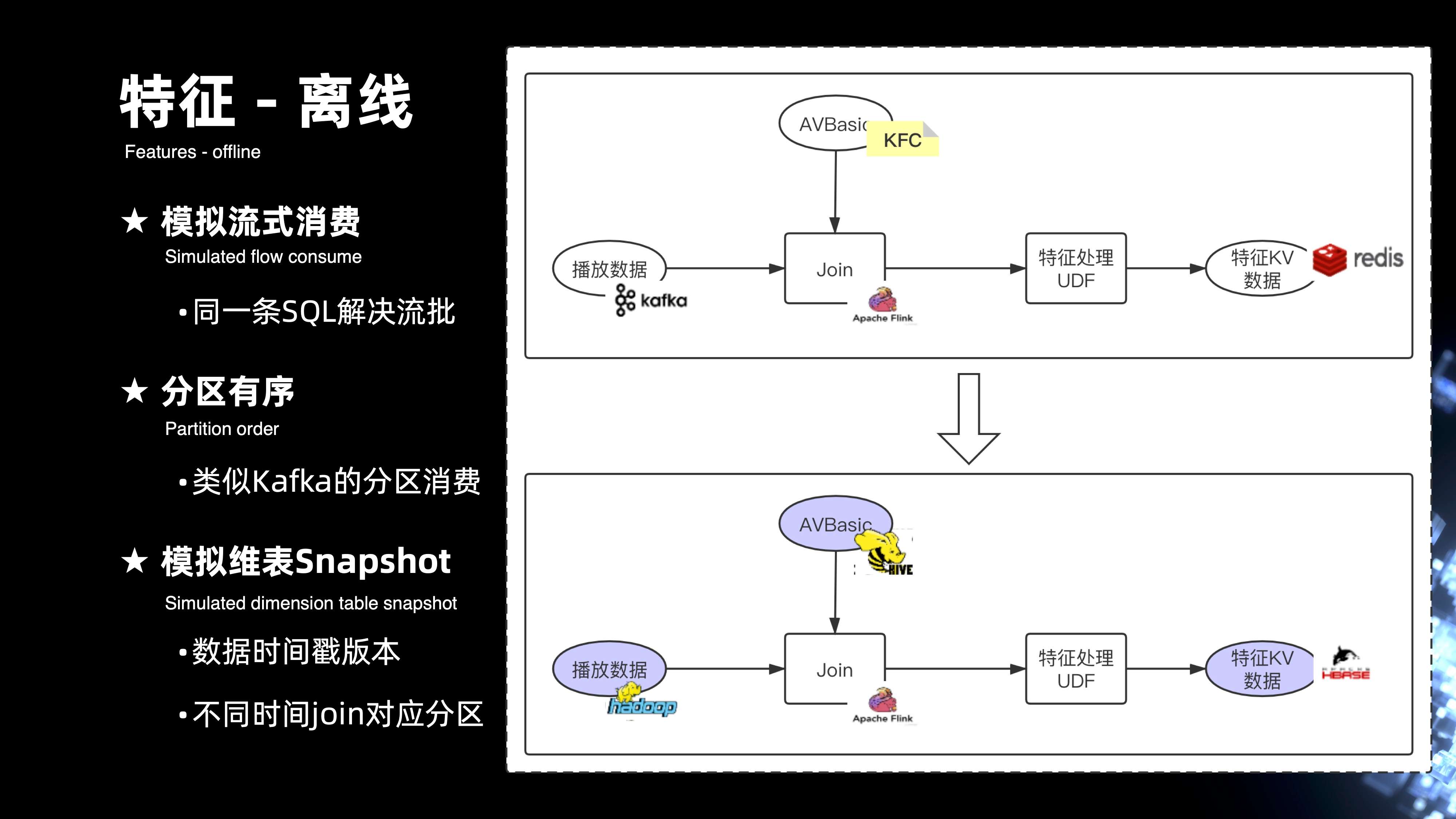
接下来看一下离线,左侧视图上半部分是完整的实时特征的计算链路,可以看出要解决同样的一条 SQL,在离线的计算上也能够复用,那就需要去解决相应的一些计算的 IO 都能够复用的问题。比如在流式上是通过 Kafka 来进行数据的输入,在离线上需要通过 HDFS 来做数据的输入。在流式上是通过 KFC 或者 AVBase 等等的一些 kv 引擎来支持,在离线上就需要通过 hive 引擎来解决,归根结底,其实需要去解决三个方面的问题:
- 第一,需要去模拟整个流式消费的能力,能够支持在离线的场景下去消费 HDFS 数据;
- 第二,需要解决 HDFS 数据在消费过程当中的分区有序的问题,类似 Kafka 的分区消费;
- 第三,需要去模拟 kv 引擎维表化的消费,实现基于 hive 的维表消费。还需要解决一个问题,当从 HDFS 拉取的每一条记录,每一条记录其实消费 hive 表的时候都有对应的 Snapshot,就相当于是每一条数据的时间戳,要消费对应数据时间戳的分区。
9. 优化
9.1 离线-分区有序
分区有序的方案其实主要是基于数据在落 HDFS 时候,前置做了一些改造。首先数据在落 HDFS 之前,是传输的管道,通过 Kafka 消费数据。在 Flink 的作业从 Kafka 拉取数据之后,通过 Eventtime 去提取数据的 watermark,每一个 Kafka Source 的并发度会将 watermark 汇报到 JobManager 当中的 GlobalWatermark 模块,GlobalAgg 会汇总来自每一个并发度 Watermark 推进的进度,从而去统计 GlobalWatermark 的进展。根据 GlobalWatermark 的进展来计算出当中有哪些并发度的 Watermark 计算过快的问题,从而通过 GlobalAgg 下发给 Kafka Source 控制信息,Kafka Source 有些并发度过快的情况下,它的整个分区推进就降低速度。这样,在 HDFS Sink 模块,在同时间片上收到的数据记录的整个 Event time 基本上有序的,最终落到 HDFS 还会在文件名上去标识它相应的分区以及相应的时间片范围。最后在 HDFS 分区目录下,就可以实现数据分区的有序目录。
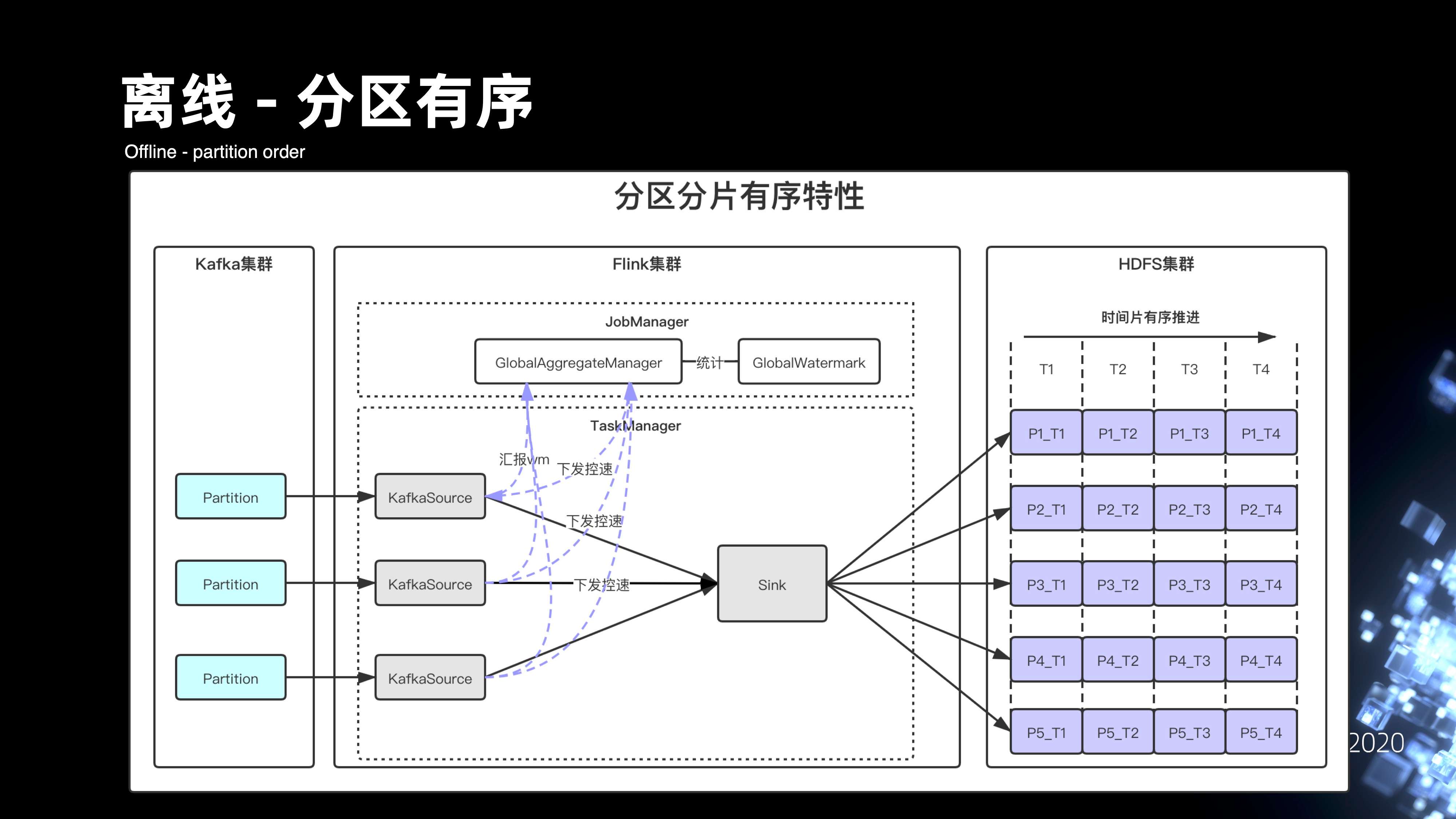
9.2 离线-分区增量消费
数据在 HDFS 增量有序之后,实现了 HDFStreamingSource,它会针对文件做 Fecher 分区,针对每个文件都有 Fecher 的线程,且每个 Fecher 线程会统计每一个文件。它 offset 处理了游标的进度,会将状态根据 Checkpoint 的过程,将它更新到的 State 当中。
这样就可以实现整个文件消费的有序推进。在回溯历史数据的时候,离线作业就会涉及到整个作业的停止。实际是在整个 FileFetcher 的模块当中去引入一个分区结束的标识,且会在每一个线程去统计每一个分区的时候,去感应它分区的结束,分区结束后的状态最后汇总到的 cancellationManager,并进一步会汇总到 Job Manager 去更新全局分区的进度,当全局所有的分区都到了末尾的游标时候,会将整个 Flink 作业进行 cancel 关闭掉。
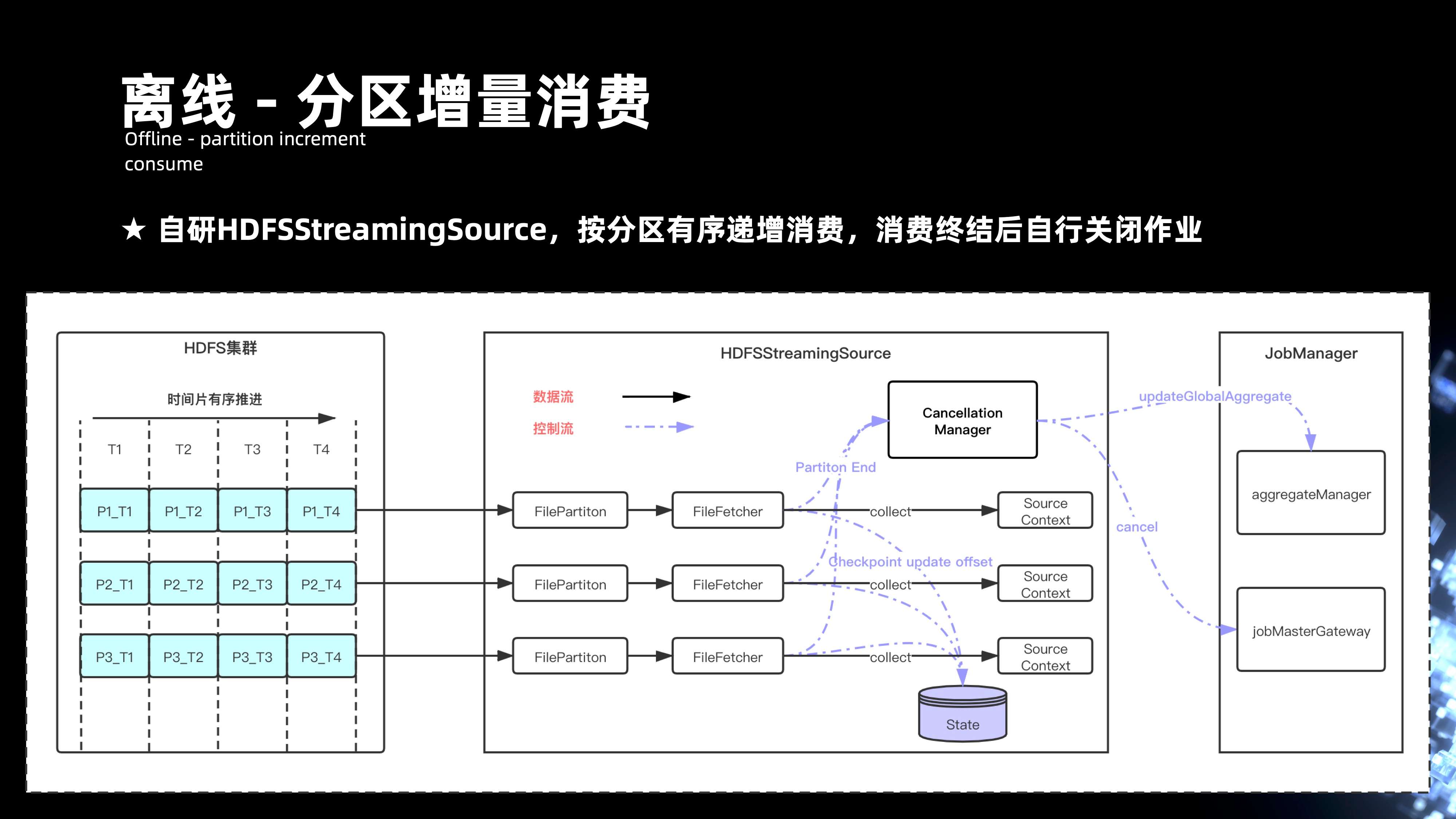
9.3 离线 - Snapshot 维表
前面讲到整个离线数据,其实数据都在 hive 上,hive 的 HDFS 表数据的整个表字段信息会非常的多,但实际做离线特征的时候,需要的信息其实是很少的,因此需要在 hive 的过程先做离线字段裁剪,将一张 ODS 的表清洗成 DW 的表,DW 的表会最后通过 Flink 运行 Job,内部会有个 reload 的 scheduler,它会定期的去根据数据当前推进的 Watermark 的分区,去拉取在 hive 当中每一个分区对应的表信息。通过去下载某 HDFS 的 hive 目录当中的一些数据,最后会在整个内存当中 reload 成 Rocksdb 的文件,Rocksdb 其实就是最后用来提供维表 KV 查询的组件。
组件里面会包含多个 Rocksdb 的 build 构建过程,主要是取决于整个数据流动的过程当中的 Eventtime,如果发现 Eventtime 推进已经快到小时分区结束的末尾时候,会通过懒加载的模式去主动 reload,构建下一个小时 Rocksdb 的分区,通过这种方式,来切换整个 Rocksdb 的读取。
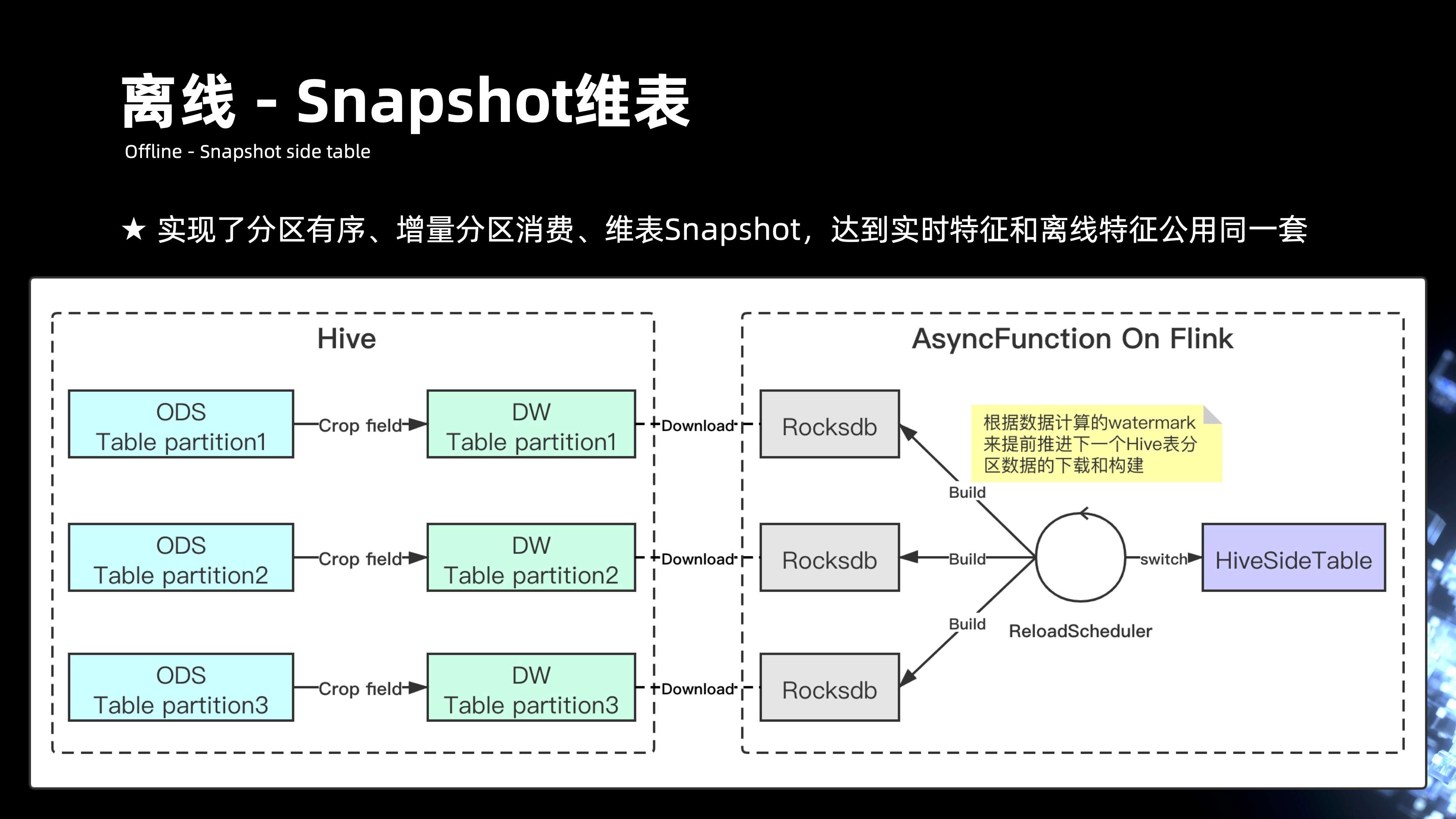
10. 实验流批一体
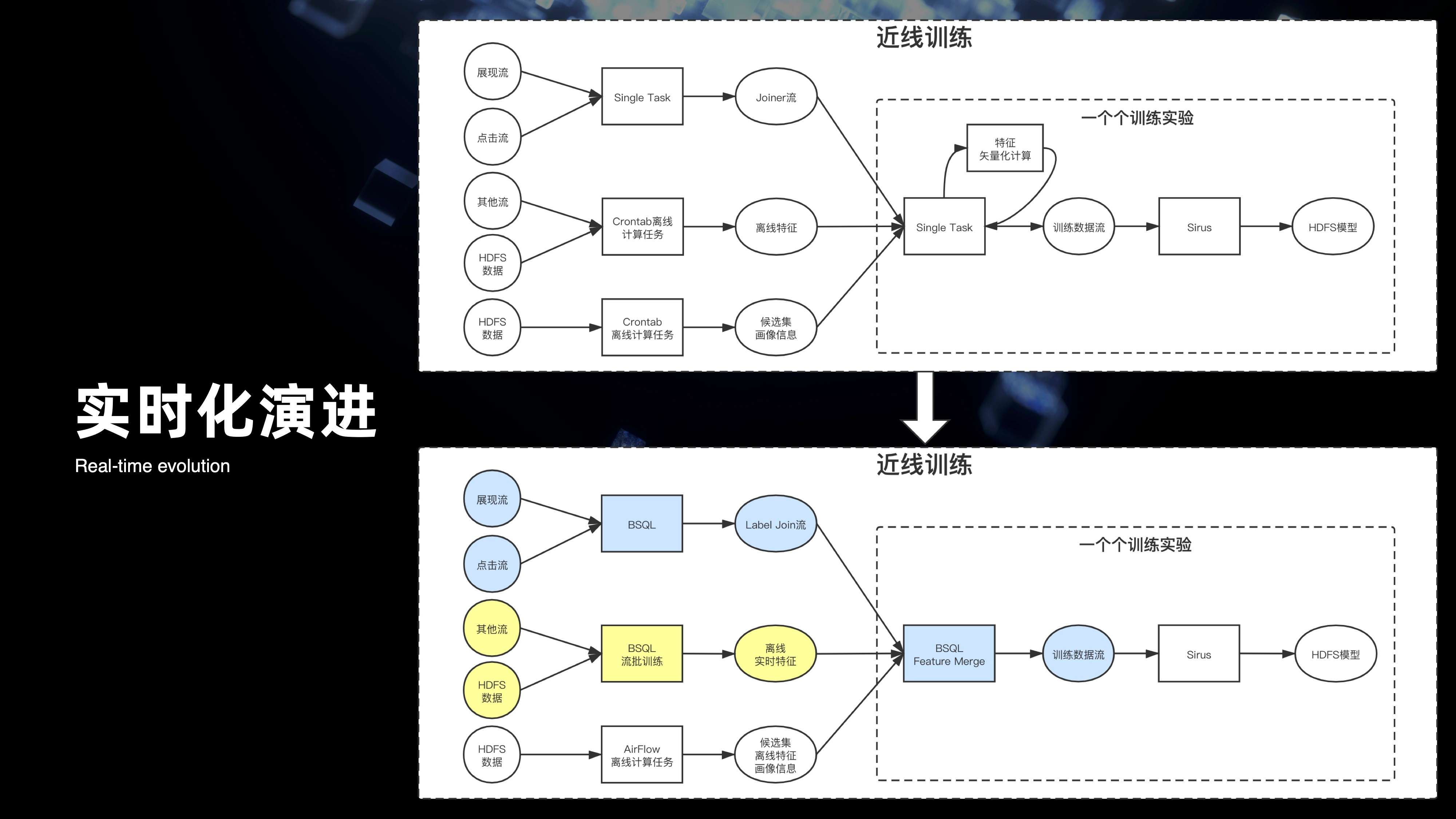
在上面三个优化,也就是分区有序增量,类 Kafka 分区 Fetch 消费,以及维表 Snapshot 的基础下,最终是实现了实时特征和离线特征,共用一套 SQL 的方案,打通了特征的流批计算。紧接着来看一下整个实验,完整的流批一体的链路,从图中可以看出最上面的粒度是整个离线的完整的计算过程。第二是整个近线的过程,离线过程其实所用计算的语义都是和近线过程用实时消费的语义是完全一致的,都是用 Flink 来提供 SQL 计算的。
来看一下近线,其实 Label join 用的是 Kafka 的一条点击流以及展现流,到了整个离线的计算链路,则用的一条 HDFS 点击的目录和 HDFS 展现目录。特征数据处理也是一样的,实时用的是 Kafka 的播放数据,以及 Hbase 的一些稿件数据。对于离线来说,用的是 hive 的稿件数据,以及 hive 的播放数据。除了整个离线和近线的流批打通,还将整个近线产生的实时的数据效果汇总到 OLAP 引擎上,通过 superset 来提供整个实时的指标可视化。其实从图可以看出完整的复杂流批一体的计算链路,当中包含的计算节点是非常的复杂和庞多的。
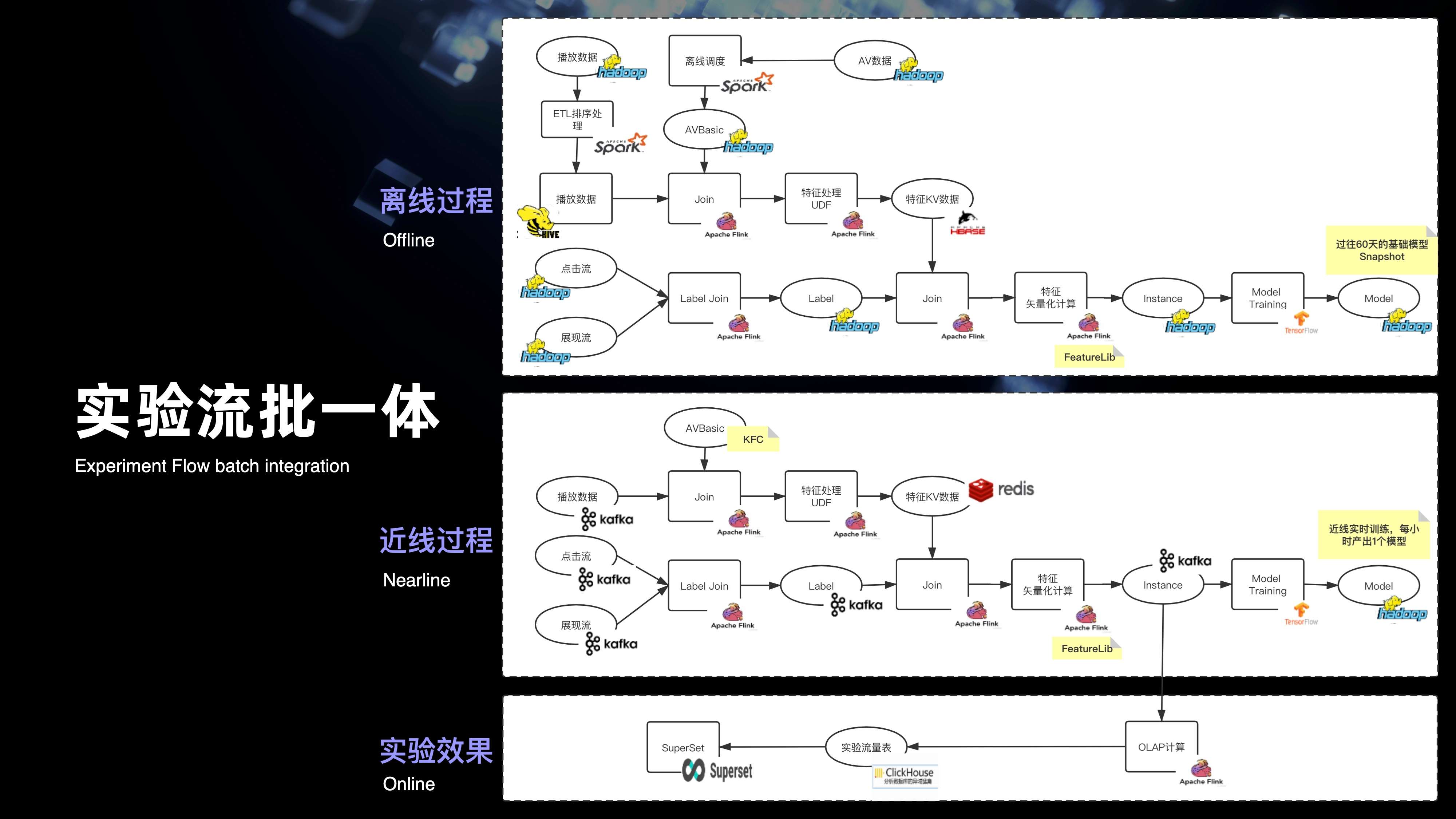
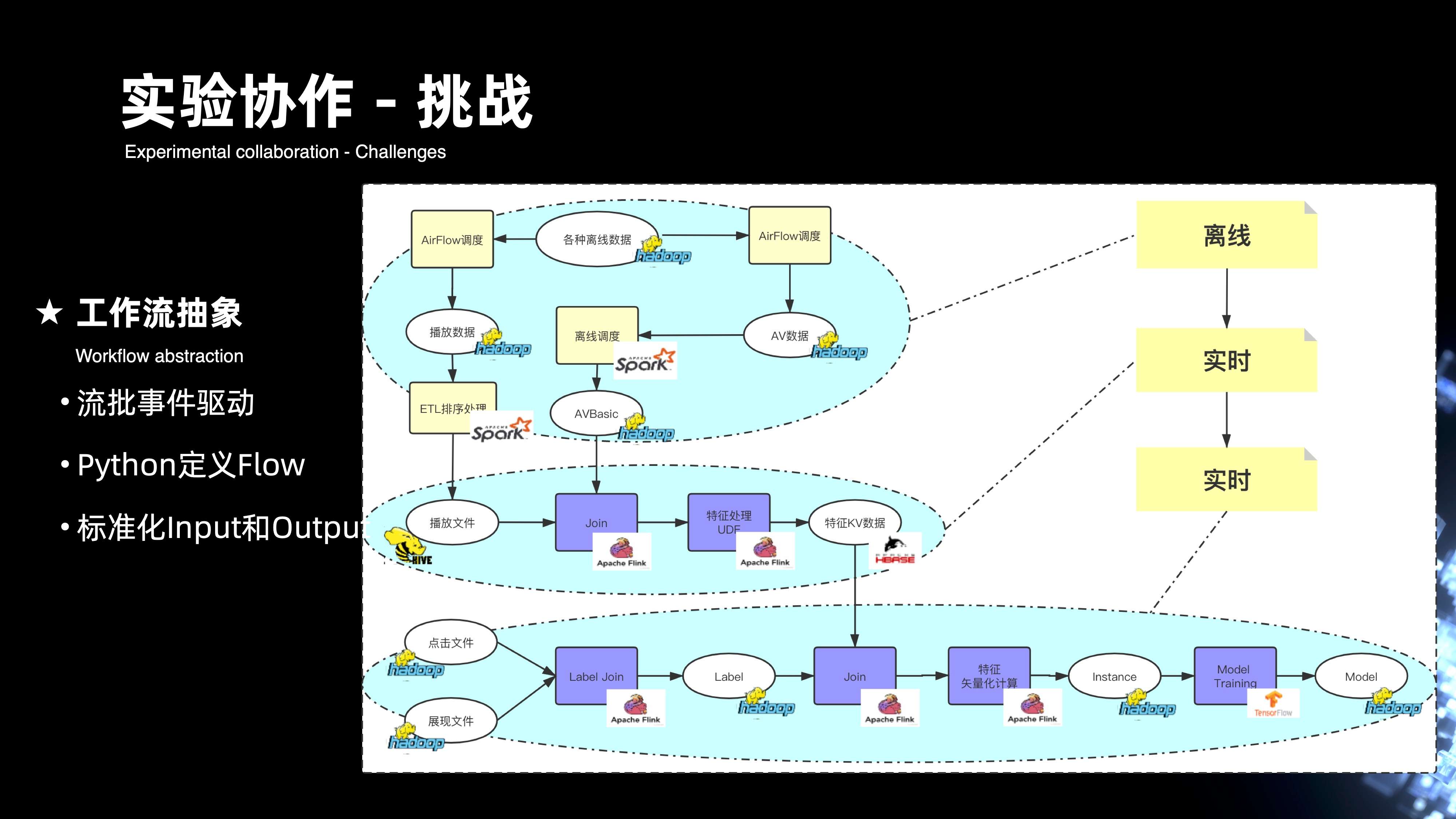
11. 实验协作 - 挑战
下阶段挑战更多是在实验协作上,下图是将前面整个链路进行简化后的抽象。从图中可以看出,三个虚线的区域框内,分别是离线的链路加两个实时的链路,三个完整的链路构成作业的流批,实际上就是一个工作流最基本的过程。里面需要去完成工作流完整的抽象,包括了流批事件的驱动机制,以及,对于算法在 AI 领域上更多希望用 Python 来定义完整的 flow,此外还将整个输入,输出以及它的整个计算趋于模板化,这样可以做到方便整个实验的克隆。
12. 引入 AIFlow
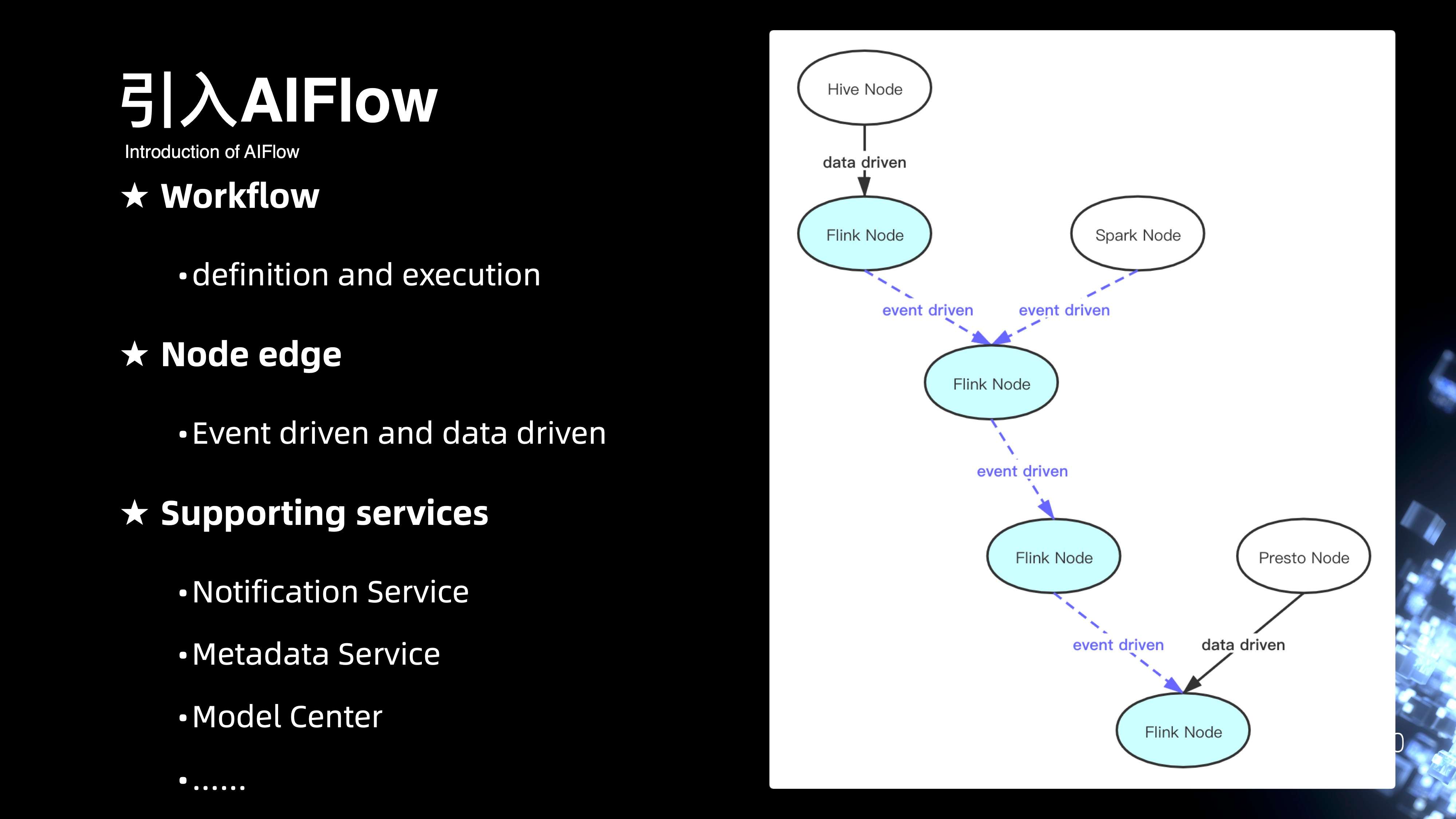
整个工作流上在下半年更多是和社区合作,引入了 AIFlow 的整套方案。
右侧其实是整个 AIFlow 完整链路的DAG视图,可以看出整个节点,其实它支持的类型是没有任何限制的,可以是流式节点,也可以是离线节点。此外的话,整个节点与节点之间通信的边是可以支持数据驱动以及事件驱动的。引入 AIFlow 的好处主要在于,AIFlow 提供基于 Python 语义来方便去定义完整的 AIFlow 的工作流,同时还包括整个工作流的进度的调度。
在节点的边上,相比原生的业界的一些 Flow 方案,他还支持基于事件驱动的整个机制。好处是可以帮助在两个 Flink 作业之间,通过 Flink 当中 watermark 处理数据分区的进度去下发一条事件驱动的消息来拉起下一个离线或者实时的作业。
此外还支持周边的一些配套服务,包括通知的一些消息模块服务,还有元数据的服务,以及在 AI 领域一些模型中心的服务。
13. Python 定义 Flow
来看一下基于 AIFlow 是如何最终定义成 Python 的工作流。右边的视图是一个线上项目的完整工作流的定义。第一、是整个是 Spark job 的定义,当中通过配置 dependence 来描述整个下游的依赖关系,它会下发一条事件驱动的消息来拉起下面的 Flink 流式作业。流式作业也同样可以通过消息驱动的方式来拉起下面的 Spark 作业。整个语义的定义非常的简单,只需要四个步骤,配置每节点的 confg 的信息,以及定义每节点的 operation 的行为,还有它的 dependency 的依赖,最后去运行整个 flow 的拓扑视图。

14. 基于事件驱动流批
接下来看一下完整的流批调度的驱动机制,下图右侧是完整的三个工作节点的驱动视图。第一个是从 Source 到 SQL 到 Sink。引入的黄色方框是扩展的 supervisor,他可以收集全局的 watermark 进度。当整个流式作业发现 watermark 可以推进到下一个小时的分区的时候,它会下发一条消息,去给到 NotifyService。NotifyService 拿到这条消息之后,它会去下发给到下一个作业,下一个作业主要会在整个 Flink 的 DAG 当中去引入 flow 的 operator,operator 在没有收到上个作业下发了消息之前,它会堵塞整个作业的运行。直到收到消息驱动之后,就代表上游其实上一个小时分区已经完成了,这时下个 flow 节点就可以驱动拉起来运作。同样,下个工作流节点也引入了 GlobalWatermark Collector 的模块来汇总收集它的处理的进度。当上一个小时分区完成之后,它也会下发一条消息到 NotifyService,NotifyService 会将这条消息去驱动调用 AIScheduler 的模块,从而去拉起 spark 离线作业来做 spark 离线的收尾。从里你们可以看出,整个链路其实是支持批到批,批到流以及流到流,以及流到批的四个场景。

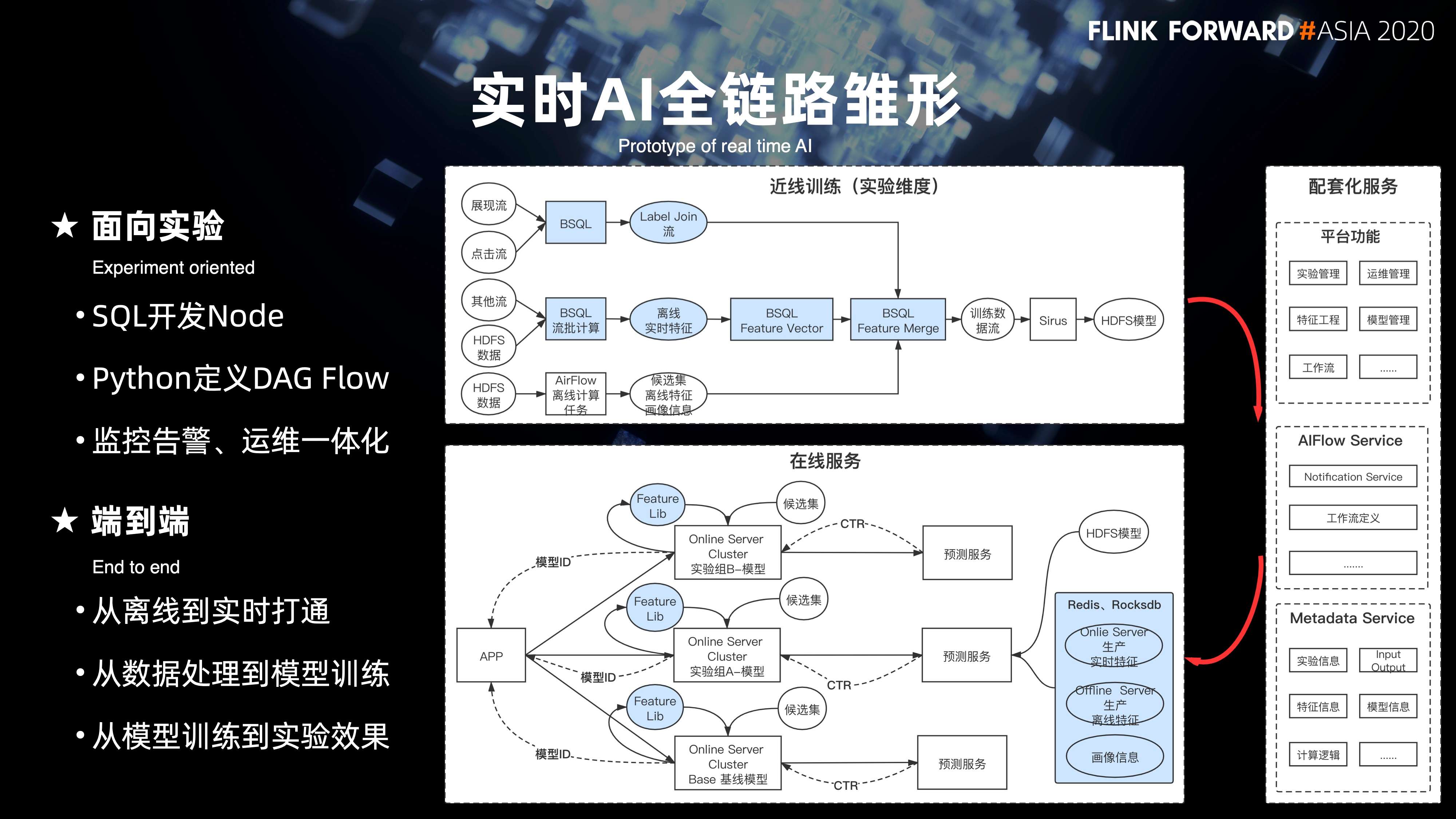
15. 实时 AI 全链路的雏形
在流和批的整个 flow 定义和调度的基础上,在 2020 年初步构建出来了实时 AI 全链路的雏形,核心是面向实验。算法同学也可以基于 SQL 来开发的 Node 的节点,Python 是可以定义完整的 DAG 工作流。监控,告警以及运维是一体化的。
同时,支持从离线到实时的打通,从数据处理到模型训练,从模型训练到实验效果的打通,以及面向端到端的打通。右侧是整个近线实验的链路。下面是将整个实验链路产出的物料数据提供给在线的预测训练的服务。整体会有三个方面的配套:
- 一是基础的一些平台功能,包括实验管理,模型管理,特征管理等等;
- 其次也包括整个 AIFlow 底层的一些 service 的服务;
- 再有是一些平台级的 metadata 的元数据服务。
四、未来的一些展望
在未来的一年,我们还会更加集中在两个方面的一些工作。
- 第一是数据湖的方向上,会集中在 ODS 到 DW 层的一些增量计算场景,以及 DW 到 ADS 层的一些场景的突破,核心会结合 Flink 加 Iceberg 以及 HUDI 来作为该方向的落地。
- 在实时 AI 平台上,会进一步去面向实验来提供一套实时的 AI 协作平台,核心是希望打造高效,能够提炼简化算法人员的工程平台。
本文为阿里云原创内容,未经允许不得转载。